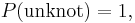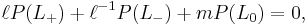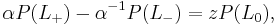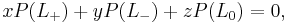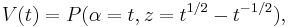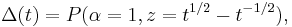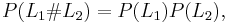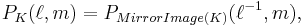HOMFLY polynomial
In the mathematical field of knot theory, the HOMFLY polynomial, sometimes called the HOMFLY-PT polynomial or the generalized Jones polynomial, is a 2-variable knot polynomial, i.e. a knot invariant in the form of a polynomial of variables m and l.
A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial, which is computed from a diagram of the knot and can be shown to be an invariant of the knot, i.e. if two diagrams have different polynomials, they represent different knots. The converse may not be true. The HOMFLY polynomial is one such invariant and it generalizes two polynomials previously discovered, the Alexander polynomial and the Jones polynomial both of which can be obtained by appropriate substitutions from HOMFLY. The HOMFLY polynomial is also a quantum invariant.
The name HOMFLY combines the initials of its co-discoverers: Jim Hoste, Adrian Ocneanu, Kenneth Millett, Peter J. Freyd, W. B. R. Lickorish, and David Nelson Yetter.[1] The addition of PT recognizes independent work carried out by Józef H. Przytycki and Paweł Traczyk.
Contents |
Definition
The polynomial is defined using skein relations:
where  are crossing and smoothing changes on a local region of a link diagram, as indicated in the figure.
are crossing and smoothing changes on a local region of a link diagram, as indicated in the figure.
The HOMFLY polynomial of a link L that is a split union of two links 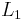 and
and 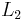 is given by
is given by 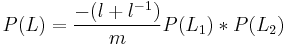 .
.
See the page on skein relation for an example of a computation using these relations.
Other HOMFLY skein relations
This polynomial can be obtained also using other skein relations:
Main properties
where V(t) is the Jones polynomial.
where  is the Alexander polynomial.
is the Alexander polynomial.
References
- ^ Freyd, P.; Yetter, D., Hoste, J., Lickorish, W.B.R., Millett, K., and Ocneanu, A. (1985). "A New Polynomial Invariant of Knots and Links". Bulletin of the American Mathematical Society 12 (2): 239–246. doi:10.1090/S0273-0979-1985-15361-3.
- Kauffman, L.H., "Formal knot theory", Princeton University Press, 1983.
- Lickorish, W.B.R. "An Introduction to Knot Theory". Springer. ISBN 038798254X.
- Weisstein, Eric W. "HOMFLY Polynomial." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/HOMFLYPolynomial.html